answer：Okay, so I have this problem where I need to find the correct derivatives of four different functions. The functions are labeled A, B, C, and D, and each has a proposed derivative. My task is to figure out which of these derivatives are correct. Let me take it step by step.Starting with option A: The function is ( frac{1}{x} ), and the proposed derivative is ( frac{1}{x^2} ). Hmm, I remember that the derivative of ( frac{1}{x} ) involves the power rule. Let me recall, the power rule states that the derivative of ( x^n ) is ( n x^{n-1} ). So, if I rewrite ( frac{1}{x} ) as ( x^{-1} ), then applying the power rule would give me ( -1 times x^{-2} ), which simplifies to ( -frac{1}{x^2} ). Wait, that's different from what's given in option A. So, option A says the derivative is ( frac{1}{x^2} ), but I just calculated it as ( -frac{1}{x^2} ). That means option A is incorrect.Moving on to option B: The function is ( cos(2x) ), and the proposed derivative is ( -2sin(2x) ). Okay, this one involves the chain rule. The chain rule is used when we have a composite function, like ( cos(u) ) where ( u = 2x ). The derivative of ( cos(u) ) with respect to ( u ) is ( -sin(u) ), and then we multiply by the derivative of ( u ) with respect to ( x ), which is 2. So, putting it all together, the derivative should be ( -2sin(2x) ). That matches exactly what's given in option B. So, option B is correct.Next is option C: The function is ( frac{3^x}{ln 3} ), and the proposed derivative is ( 3^x ). Alright, this one involves the derivative of an exponential function. I remember that the derivative of ( a^x ) with respect to ( x ) is ( a^x ln(a) ). So, if I have ( 3^x ), its derivative would be ( 3^x ln(3) ). But in the function given, it's ( frac{3^x}{ln 3} ). So, taking the derivative, it would be ( frac{3^x ln(3)}{ln 3} ), which simplifies to ( 3^x ). That's exactly what's given in option C. So, option C is correct.Lastly, option D: The function is ( lg x ), which I believe is the logarithm base 10 of ( x ), and the proposed derivative is ( frac{-1}{x ln 10} ). Let me think about the derivative of a logarithm. The general rule is that the derivative of ( log_a(x) ) is ( frac{1}{x ln(a)} ). So, for ( lg x ), which is ( log_{10}(x) ), the derivative should be ( frac{1}{x ln(10)} ). But option D has a negative sign in the numerator, making it ( frac{-1}{x ln(10)} ). That doesn't match my calculation. So, option D is incorrect.To summarize:- Option A: Incorrect, the derivative should be ( -frac{1}{x^2} ).- Option B: Correct.- Option C: Correct.- Option D: Incorrect, the derivative should be ( frac{1}{x ln(10)} ).Therefore, the correct options are B and C.

answer：Okay, so I have this problem where I need to figure out if two numbers, x and y, are in a set M. The set M is defined as all numbers of the form a + sqrt(2)*b, where a and b are rational numbers. That means any number in M can be written with a rational part and a part that's a multiple of sqrt(2) with another rational coefficient. First, let me look at x. It's given as 1 divided by (3 - 5*sqrt(2)). Hmm, that looks a bit complicated because of the square root in the denominator. I remember from algebra that when you have a denominator with a square root, you can rationalize it by multiplying the numerator and the denominator by the conjugate of the denominator. The conjugate of (3 - 5*sqrt(2)) is (3 + 5*sqrt(2)). So, if I multiply both the top and bottom by that, I should be able to get rid of the square root in the denominator.Let me write that out:x = 1 / (3 - 5*sqrt(2)) Multiply numerator and denominator by (3 + 5*sqrt(2)):x = [1 * (3 + 5*sqrt(2))] / [(3 - 5*sqrt(2))(3 + 5*sqrt(2))]Now, let's compute the denominator. It's a difference of squares, so (a - b)(a + b) = a² - b². Here, a is 3 and b is 5*sqrt(2). So:Denominator = 3² - (5*sqrt(2))² = 9 - (25 * 2) = 9 - 50 = -41So, the denominator simplifies to -41. Now, the numerator is just 3 + 5*sqrt(2). So putting it all together:x = (3 + 5*sqrt(2)) / (-41) = -3/41 - (5/41)*sqrt(2)Okay, so x is equal to -3/41 minus (5/41) times sqrt(2). Both -3/41 and -5/41 are rational numbers, right? Because they are fractions of integers. So, that means x can be written as a + sqrt(2)*b where a and b are both rational. Therefore, x is in set M.Alright, that takes care of x. Now, let's look at y. It's given as 3 + sqrt(2)*pi. Hmm, pi is an irrational number, approximately 3.14159..., but it's not a rational number. So, let's see if y can be expressed in the form a + sqrt(2)*b with a and b rational.Looking at y, it's 3 plus sqrt(2) times pi. So, if I try to write this as a + sqrt(2)*b, then a would be 3 and b would be pi. But pi is not a rational number. Since b has to be rational for y to be in set M, and pi isn't rational, y cannot be expressed in that form. Therefore, y is not in set M.Wait, let me double-check that. Is there any way to express sqrt(2)*pi as a multiple of sqrt(2) with a rational coefficient? Well, pi is just a constant, and it's irrational. So, unless pi can be expressed as a rational number, which it can't, then b would have to be irrational. So, yeah, y isn't in M.So, to recap: x can be written as a + sqrt(2)*b with a and b rational, so x is in M. y cannot be written in that form because it involves pi, which is irrational, so y is not in M.Therefore, the correct answer should be option B: x is in M, y is not in M.**Final Answer**boxed{B}

answer：Okay, so I have this problem about purchasing Olympic mascots, Bing Dwen Dwen and Shuey Rhon Rhon. It's divided into two parts. Let me try to understand and solve each part step by step.**Part 1: Finding the value of m**First, the problem says that the quantity of Bing Dwen Dwen mascots purchased for 3000 yuan is the same as the quantity of Shuey Rhon Rhon mascots purchased for 2400 yuan. Hmm, okay. So, if I spend 3000 yuan on Bing Dwen Dwen, I get a certain number of them, and if I spend 2400 yuan on Shuey Rhon Rhon, I get the same number. That means the number of each mascot I can buy with those amounts is equal.Let me denote the purchase price of Bing Dwen Dwen as m yuan per each, and Shuey Rhon Rhon as m - 30 yuan per each, since it's given in the table.So, the quantity of Bing Dwen Dwen I can buy with 3000 yuan is 3000 divided by m, which is 3000/m.Similarly, the quantity of Shuey Rhon Rhon I can buy with 2400 yuan is 2400 divided by (m - 30), which is 2400/(m - 30).Since these quantities are equal, I can set up the equation:3000/m = 2400/(m - 30)Now, I need to solve for m. Let me cross-multiply to get rid of the fractions:3000 * (m - 30) = 2400 * mExpanding both sides:3000m - 90000 = 2400mNow, subtract 2400m from both sides:3000m - 2400m - 90000 = 0Which simplifies to:600m - 90000 = 0Adding 90000 to both sides:600m = 90000Dividing both sides by 600:m = 90000 / 600Calculating that:m = 150So, the value of m is 150 yuan. Let me just check if this makes sense. If m is 150, then Shuey Rhon Rhon is 150 - 30 = 120 yuan each.Now, checking the quantities:3000 / 150 = 202400 / 120 = 20Yes, both give 20 mascots. So, that checks out.**Part 2: Maximizing profit with constraints**Now, the second part is about purchasing a total of 200 mascots, with the condition that the quantity of Shuey Rhon Rhon must not be less than 2/3 of the quantity of Bing Dwen Dwen. We need to figure out how many of each to buy to maximize profit.First, let me note the selling prices:- Bing Dwen Dwen: 190 yuan each- Shuey Rhon Rhon: 140 yuan eachWe already found m = 150, so the purchase prices are:- Bing Dwen Dwen: 150 yuan each- Shuey Rhon Rhon: 120 yuan eachLet me denote:Let x be the number of Bing Dwen Dwen mascots purchased.Then, the number of Shuey Rhon Rhon mascots purchased will be 200 - x.But there's a constraint: the quantity of Shuey Rhon Rhon must be at least 2/3 of the quantity of Bing Dwen Dwen.So, mathematically, that is:200 - x ≥ (2/3)xLet me solve this inequality.First, multiply both sides by 3 to eliminate the fraction:3*(200 - x) ≥ 2xWhich is:600 - 3x ≥ 2xNow, add 3x to both sides:600 ≥ 5xDivide both sides by 5:120 ≥ xSo, x ≤ 120Therefore, the maximum number of Bing Dwen Dwen mascots we can purchase is 120, and the minimum number of Shuey Rhon Rhon is 200 - 120 = 80.Now, to maximize profit, let's calculate the profit per mascot.Profit per Bing Dwen Dwen is selling price - purchase price:190 - 150 = 40 yuan per mascotProfit per Shuey Rhon Rhon is:140 - 120 = 20 yuan per mascotSo, for each Bing Dwen Dwen, we make 40 yuan, and for each Shuey Rhon Rhon, we make 20 yuan.To maximize profit, since Bing Dwen Dwen gives a higher profit per unit, we should try to buy as many as possible within the constraints.Given that x ≤ 120, the maximum x is 120. So, purchasing 120 Bing Dwen Dwen and 80 Shuey Rhon Rhon.Let me calculate the total profit:Profit from Bing Dwen Dwen: 120 * 40 = 4800 yuanProfit from Shuey Rhon Rhon: 80 * 20 = 1600 yuanTotal profit: 4800 + 1600 = 6400 yuanIs this the maximum? Let me see if buying fewer Bing Dwen Dwen and more Shuey Rhon Rhon would give a higher profit.But since each Bing Dwen Dwen gives 40 yuan, which is double the 20 yuan from Shuey Rhon Rhon, it's better to maximize Bing Dwen Dwen.Wait, but the constraint is that Shuey Rhon Rhon must be at least 2/3 of Bing Dwen Dwen. So, if we try to buy more Bing Dwen Dwen, say x = 121, then Shuey Rhon Rhon would be 79.But 79 < (2/3)*121 ≈ 80.666, which is not allowed. So, 120 is the maximum x allowed.Therefore, purchasing 120 Bing Dwen Dwen and 80 Shuey Rhon Rhon gives the maximum profit of 6400 yuan.I think that's the solution. Let me just recap:1. Found m by setting up the equation based on equal quantities purchased with different amounts.2. Solved the equation to find m = 150.3. For the second part, set up the variables, considered the constraint, calculated the profit per unit, and determined that buying as many Bing Dwen Dwen as allowed within the constraint would maximize profit.Everything seems to check out.

answer：Alright, so I've got this problem about a function ( f(x) ) defined on all real numbers. It has this property that for any real numbers ( x ) and ( y ), ( f(x + y) = f(x) cdot f(y) ). Also, it's given that for ( x < 0 ), ( f(x) > 1 ). Part (1) asks me to prove that for ( x > 0 ), ( 0 < f(x) < 1 ). Hmm, okay. Let me think about this. So, the function has this multiplicative property over addition, which reminds me of exponential functions because ( e^{x+y} = e^x cdot e^y ). But here, it's a general function, not necessarily exponential. First, maybe I should check what ( f(0) ) is. If I plug in ( x = 0 ) and ( y = 0 ), then ( f(0 + 0) = f(0) cdot f(0) ), so ( f(0) = [f(0)]^2 ). That implies ( f(0) ) is either 0 or 1. But if ( f(0) = 0 ), then for any ( x ), ( f(x) = f(x + 0) = f(x) cdot f(0) = 0 ), which would make the function identically zero. But that contradicts the condition that for ( x < 0 ), ( f(x) > 1 ). So, ( f(0) ) must be 1.Okay, so ( f(0) = 1 ). Now, for ( x > 0 ), I need to show ( 0 < f(x) < 1 ). Given that for ( x < 0 ), ( f(x) > 1 ), maybe I can relate ( f(x) ) for positive ( x ) to ( f(-x) ) which is greater than 1.Let me consider ( f(x) cdot f(-x) = f(x + (-x)) = f(0) = 1 ). So, ( f(x) cdot f(-x) = 1 ). Since ( f(-x) > 1 ) (because ( -x < 0 ) when ( x > 0 )), then ( f(x) = frac{1}{f(-x)} ). Since ( f(-x) > 1 ), ( frac{1}{f(-x)} ) must be between 0 and 1. Therefore, ( 0 < f(x) < 1 ) for ( x > 0 ). That seems to work.Moving on to part (2), which asks to determine the monotonicity of ( f(x) ). Monotonicity means whether the function is increasing or decreasing. Given that for negative ( x ), ( f(x) > 1 ), and for positive ( x ), ( 0 < f(x) < 1 ), it suggests that as ( x ) increases, ( f(x) ) decreases. Let me test this. Suppose ( x_1 < x_2 ). Then ( x_2 - x_1 > 0 ), so ( f(x_2 - x_1) < 1 ). Then, ( f(x_2) = f(x_1 + (x_2 - x_1)) = f(x_1) cdot f(x_2 - x_1) ). Since ( f(x_2 - x_1) < 1 ), multiplying ( f(x_1) ) by something less than 1 would make ( f(x_2) < f(x_1) ). So, ( f(x) ) is decreasing.Okay, that makes sense. So, the function is monotonically decreasing.Now, part (3) is a bit trickier. It says that for any real numbers ( x, y ), ( f(x^2) cdot f(y^2) leq f(a x y) ) always holds. I need to find the range of the real number ( a ).First, let's recall that ( f ) is multiplicative: ( f(x + y) = f(x) f(y) ). Also, since ( f ) is decreasing, if ( x leq y ), then ( f(x) geq f(y) ).Given the inequality ( f(x^2) cdot f(y^2) leq f(a x y) ), let's rewrite the left side using the multiplicative property. Since ( f(x^2) cdot f(y^2) = f(x^2 + y^2) ). So, the inequality becomes ( f(x^2 + y^2) leq f(a x y) ).Since ( f ) is decreasing, this inequality implies that ( x^2 + y^2 geq a x y ). Because if ( f(u) leq f(v) ), then ( u geq v ) since ( f ) is decreasing.So, we have ( x^2 + y^2 geq a x y ) for all real numbers ( x, y ). This is a quadratic inequality in terms of ( x ) and ( y ). Let me think about how to find the range of ( a ) such that this inequality holds for all real ( x, y ).One approach is to consider this as a quadratic in one variable, say ( x ), treating ( y ) as a constant. So, rearranging:( x^2 - a y x + y^2 geq 0 ).For this quadratic to be non-negative for all ( x ), the discriminant must be less than or equal to zero. The discriminant ( D ) is ( ( -a y )^2 - 4 cdot 1 cdot y^2 = a^2 y^2 - 4 y^2 = y^2 (a^2 - 4) ).For the quadratic to be non-negative for all ( x ), the discriminant must satisfy ( D leq 0 ). So, ( y^2 (a^2 - 4) leq 0 ).Since ( y^2 ) is always non-negative, the inequality ( y^2 (a^2 - 4) leq 0 ) holds if and only if ( a^2 - 4 leq 0 ), which implies ( a^2 leq 4 ), so ( |a| leq 2 ). Therefore, ( a ) must be in the interval ( [-2, 2] ).Let me double-check this. If ( a = 2 ), then the inequality becomes ( x^2 + y^2 geq 2 x y ), which is ( (x - y)^2 geq 0 ), always true. Similarly, for ( a = -2 ), it becomes ( x^2 + y^2 geq -2 x y ), which is ( x^2 + 2 x y + y^2 = (x + y)^2 geq 0 ), also always true. For values of ( a ) between -2 and 2, the inequality should hold as well because the coefficient on ( x y ) is smaller in magnitude, making the left side larger.If ( |a| > 2 ), say ( a = 3 ), then for ( x = y = 1 ), we have ( 1 + 1 = 2 ) and ( 3 cdot 1 cdot 1 = 3 ), so ( 2 geq 3 ) is false. Hence, ( |a| ) cannot exceed 2.So, the range of ( a ) is ( -2 leq a leq 2 ).**Final Answer**(1) boxed{0 < f(x) < 1}(2) The function ( f(x) ) is monotonically decreasing.(3) The range of ( a ) is boxed{[-2, 2]}.

answer：First, I recognize that p is 20% more efficient than q. This means that p can do 1.2 times the work that q can do in the same amount of time.Next, I know that p can complete the work in 22 days. Therefore, p's work rate is 1/22 of the work per day.Using the efficiency relationship, I can determine q's work rate. Since p's work rate is 1.2 times q's work rate, I can set up the equation 1/22 = 1.2 * q's work rate and solve for q's work rate.Once I have both p's and q's work rates, I add them together to find the combined work rate when they work together.Finally, to find the total number of days required to complete the work together, I take the reciprocal of the combined work rate.

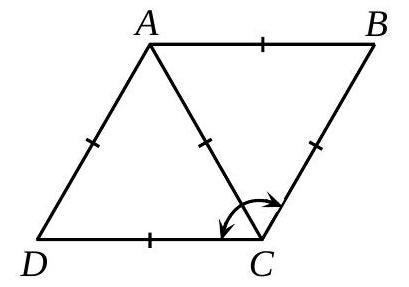
answer：Alright, so I've got this problem here about a rhombus (ABCD), and I need to find the measure of angle (BCD). The options are (60^circ), (90^circ), (120^circ), (45^circ), and (160^circ). Hmm, okay, let's break this down step by step.First, I remember that a rhombus is a type of quadrilateral where all four sides are equal in length. That's one of its defining properties. Also, in a rhombus, opposite angles are equal, and adjacent angles are supplementary, meaning they add up to (180^circ). So, if I can find one angle, I can figure out the others.Now, the problem mentions a diagram, but since I can't see the diagram, I need to rely on the properties of a rhombus. I also recall that the diagonals of a rhombus bisect each other at right angles. That means they cut each other exactly in half and form four right angles where they intersect. Additionally, each diagonal bisects two opposite angles. So, if I can figure out the angles formed by the diagonals, I can find the measure of angle (BCD).Let me try to visualize the rhombus (ABCD). Let's label the vertices in order: (A), (B), (C), and (D). So, sides (AB), (BC), (CD), and (DA) are all equal. The diagonals would be (AC) and (BD), intersecting at point (O), which is the midpoint of both diagonals.Since the diagonals bisect each other at right angles, triangles (AOB), (BOC), (COD), and (DOA) are all right-angled triangles. Each of these triangles has sides that are halves of the diagonals and a side of the rhombus.Now, if I can find the measure of one of the angles at the vertices, I can determine the measure of angle (BCD). Let's assume that the diagonals create some specific angles. For instance, if one of the angles formed by the diagonals is (60^circ), then the adjacent angle would be (120^circ) because they are supplementary.Wait, the problem doesn't give me any specific information about the lengths of the sides or the diagonals. So, how can I determine the measure of angle (BCD)? Maybe I need to recall that in a rhombus, the diagonals not only bisect each other at right angles but also bisect the vertex angles.So, if I consider angle (BCD), it is formed by sides (BC) and (CD). The diagonal (BD) bisects this angle into two equal parts. If I can find the measure of one of these bisected angles, I can double it to find the measure of angle (BCD).But without specific measurements, I need to rely on the properties of the rhombus and the given options. Let's think about the possible measures. If the rhombus were a square, all angles would be (90^circ), but a square is a special case of a rhombus. However, since the options include (60^circ) and (120^circ), it's likely that the rhombus is not a square.If angle (BCD) is (60^circ), then the adjacent angle (ABC) would be (120^circ) because they are supplementary. Similarly, if angle (BCD) is (120^circ), then angle (ABC) would be (60^circ). Since the options include both (60^circ) and (120^circ), I need to figure out which one is the correct measure.Wait, maybe I can use the fact that the diagonals bisect the angles. If angle (BCD) is (120^circ), then each of the angles formed by the diagonal (BD) would be (60^circ). Similarly, if angle (BCD) is (60^circ), then each of the angles formed by the diagonal would be (30^circ). But since the diagonals intersect at right angles, the triangles formed would have angles of (90^circ), (60^circ), and (30^circ), which are common in 30-60-90 triangles.Given that, if the diagonals create 60-degree angles, then the original angle (BCD) would be (120^circ). That seems to make sense because the bisected angles would each be (60^circ), adding up to (120^circ) for angle (BCD).Alternatively, if the diagonals created 30-degree angles, then angle (BCD) would be (60^circ). But since the options include both, I need to determine which one is correct based on the properties of the rhombus.Wait, another thought: in a rhombus, the diagonals are not equal unless it's a square. So, if the diagonals are of different lengths, the angles they create would also be different. If one diagonal is longer than the other, the angles it creates would be larger.Given that, if the longer diagonal creates larger angles, then angle (BCD) would be (120^circ) because it's larger than (60^circ). That seems plausible.Also, considering that the sum of all angles in a quadrilateral is (360^circ), if angle (BCD) is (120^circ), then the opposite angle (BAD) would also be (120^circ), and the other two angles (ABC) and (ADC) would each be (60^circ). That adds up correctly: (120 + 120 + 60 + 60 = 360^circ).Alternatively, if angle (BCD) were (60^circ), then the opposite angle would also be (60^circ), and the other two angles would be (120^circ) each. That also adds up to (360^circ). So, both scenarios are possible.But how do I determine which one is the case here? Maybe I need to consider the properties of the diagonals again. If the diagonals bisect the angles, and if angle (BCD) is (120^circ), then the diagonal (BD) would create two angles of (60^circ) each at point (C). Similarly, the diagonal (AC) would bisect angle (ABC) into two angles of (30^circ) each if angle (ABC) is (60^circ).Wait, but in a rhombus, the diagonals are not necessarily equal, but they do intersect at right angles. So, if one diagonal is longer, it would create larger angles. If angle (BCD) is (120^circ), then the diagonal (BD) is longer than diagonal (AC), creating larger angles at the vertices.Alternatively, if angle (BCD) is (60^circ), then diagonal (BD) is shorter, creating smaller angles.Given that, and considering the options, I think the more likely answer is (120^circ) because it's a more common measure in rhombuses that are not squares, especially when considering the properties of the diagonals creating 60-degree angles.Wait, but I'm not entirely sure. Maybe I should think about the triangle formed by the diagonals. If I consider triangle (BCD), it's actually not a triangle because (B), (C), and (D) are vertices of the rhombus, so it's part of the rhombus itself.Alternatively, if I look at triangle (BCO), where (O) is the intersection of the diagonals, then triangle (BCO) is a right-angled triangle with angles (90^circ), (60^circ), and (30^circ). If that's the case, then angle (BCD) would be (120^circ) because it's made up of two (60^circ) angles from the diagonals.Yes, that makes sense. So, each diagonal bisects the angle into two equal parts, and if each part is (60^circ), then the whole angle is (120^circ).Therefore, I think the measure of angle (BCD) is (120^circ).